Math 322, Mathematical Analysis for Engineers, Fall 2017
Complex functions and integration, line and surface integrals,
Fourier series, partial differential equations.
All visualization below are done using Maxima computer algebra system (CAS).
Cart simulation
This is a simulation of a differential equation for the displacement $y=y(t)$ of a cart ensemble, consisting of a cart of mass $m$, a spring with spring constant $k$ and a damper with damping constant $b$. \[ m\,y'' + b\,y'+k\,y = f(t) \] where \[ f(t)=f_0\,\sin(2\pi\omega\,t)\] i.e. the cart is subjected to an external periodic force.
Joukovski map
This is the conformal map: \[ J(z)=z+\frac{1}{z} \] Shown is the mapping the circle $|z-a|=|1-a|$ (blue) to an airfoil (red). The number $a$ (the center) varies over an interval in the complex domain.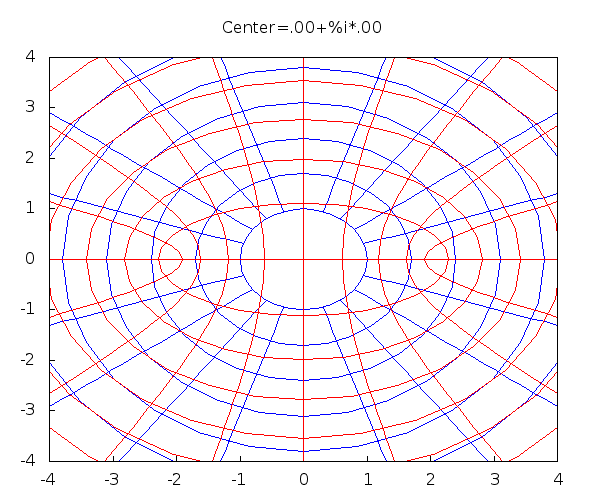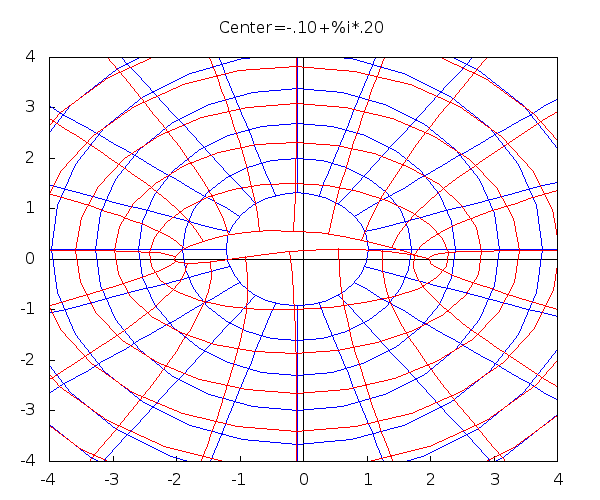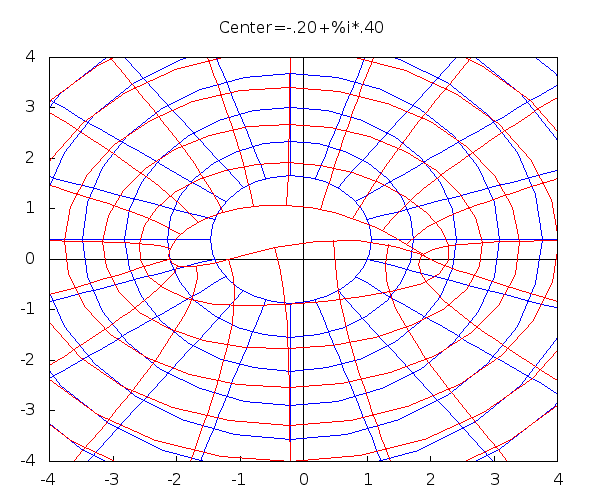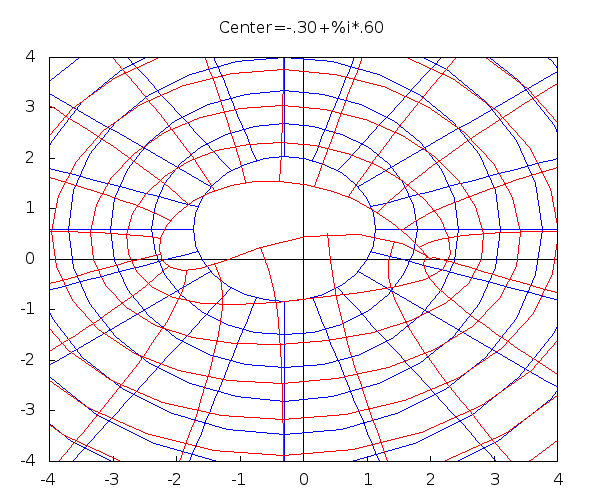
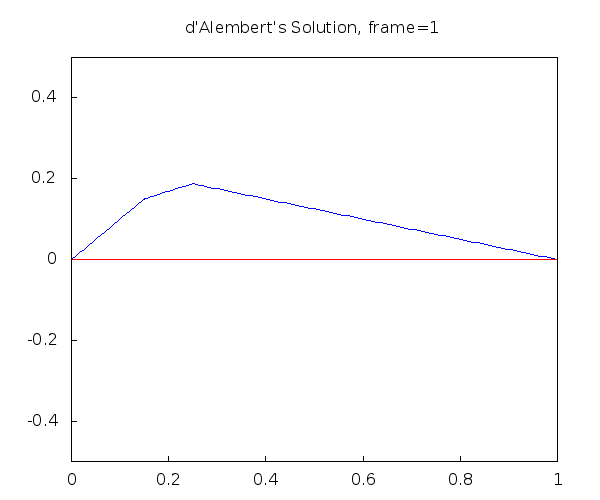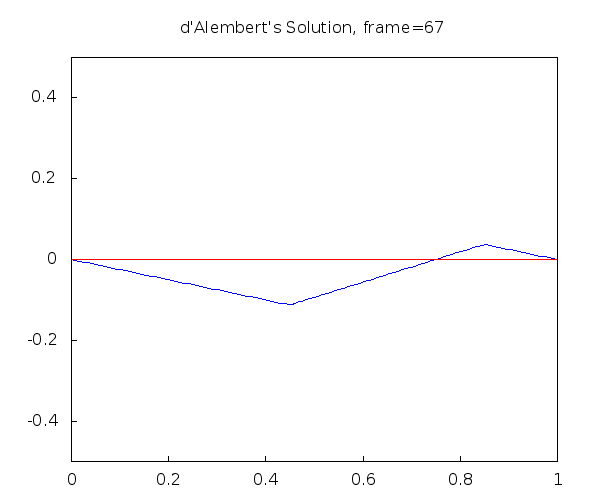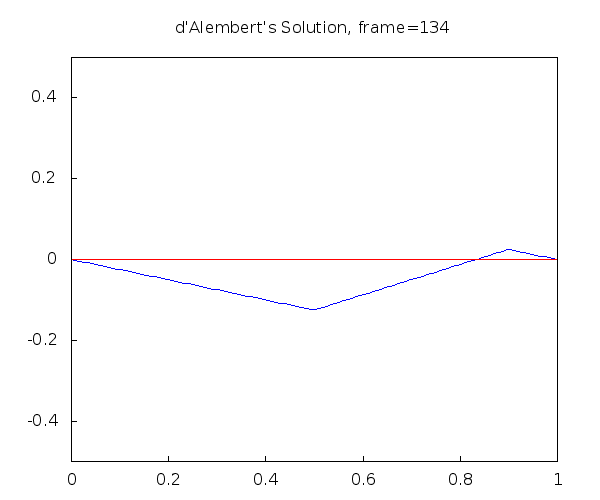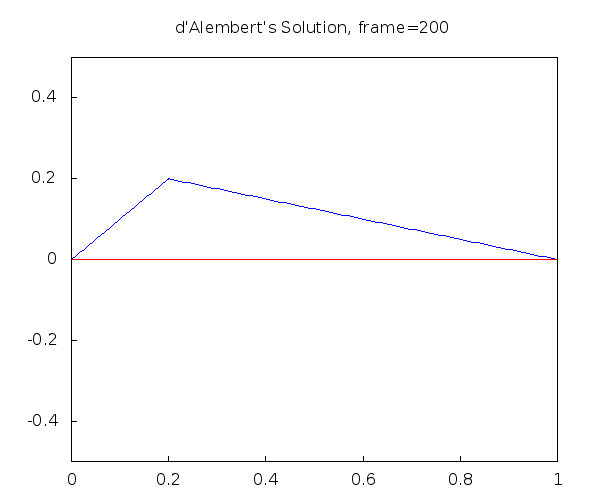
D'Alembert's Solution of the Wave Equation with Maxima
String plucked in the middle

String plucked at 20% of the string length