The beginnings
The equichordal point problem was posed in 1916 by Fujiwara
and in the subsequent article by Blaschke, Rothe and
Weitzenböck in 1917. The formulation sounds like a puzzle
in a geometry textbook. It starts with the following definition:
A point inside a closed, planar curve is called an equichordal point if every
chord passing through that point has the same length.
For example, the center of a circle is equichordal, as every chord
passing through the center has length equal to the circle diameter.
One should note that a chord is simply a segment connecting two points
on the curve.
Fujiwara himself observed that there are many curves, other
than a circle, that have at least one equichordal point. He
also proved that there is no curve with three equichordal
points.
After the work of Fujiwara, the only open case left was that
of the two equichordal points. This is essentially the
equichordal point problem. There are some problems with
interpreting the problem for an arbitrary simple closed curve
(i.e. a curve without intersections). The notion of convexity
was used to resolve these issues. We recall that a curve is
convex if it is a boundary of a 2-dimensional region which is
convex. A region is convex if every two points in the region
can be connected with a line segment which is totally
contained in the region.
The Equichordal Point Problem:
Is there a convex planar curve with two equichordal points?
There have been many attempts at solving the problem between
1916 and 1996, when I published a full solution of the
problem. In fact, the attempts continue to this day! They are
mostly by mathematical enthusiasts who find the problem
appealing.
All in-depth studies of the problem have indicated
that the methods of its solution probably must be outside the
scope of elementary mathematics. In fact, the current solution
utilizes methods from three areas of mathematics: dynamical
systems, complex analysis and algebraic geometry. Some brand
new math had to be developed to handle the problem's
difficulty.
A famous quote by Rogers in regard to the difficulty of the
problem some time before it was solved:
If you are interested in studying the problem, my first advice is: "Don't".
There is even an article by V. Klee written in the 1960's, who listed the problem
along with Fermat's Last Theorem and Riemann Hypothesis as
one of "the" three research problems.
The most mature attempt was in a paper by Shaefke and Volkmer
in 1991. The authors used methods of advanced asymptotic
analysis called "perturbation theory beyond all orders" which
allowed them to show that there are no equichordal curves
of small eccentricity (the relative distance of the two
equichordal points).
The paper opened a realistic path to a computer-assisted solution of
the problem. However, to the best of my knowledge, the computer
assisted proof has not been completed.
My main theorem on the subject of equichordal points shows
that the problem has little to do with convexity.
The class of curves are star-shaped curves
with respect to the two equichordal points.
Here is the relevant definition:
A simple closed planar curve is called star-shaped
with respect to a certain point P if
every point in the region bounded by the curve
can be connected to P with a line segment
entirely contained within the region.
With this definition, we are ready to formulate the theorem,
which summarizes the results of the original article:
Rychlik, M. "A Complete Solution to the Equichordal Problem
of Fujiwara, Blaschke, Rothe, and Weitzenböck." Inventiones
Mathematicae (129), 141-212, 1997.
Here is the precise statement of the theorem:
For every two points O1 and
O2 of the plane, and
all simple planar curves C such that
C is star-shaped with respect to both
O1 and O2,
it cannot be true that both these points are
equichordal.
With less precision, we may simply say that
there are no curves with two equichordal points.
Thus, the answer to the original question is negative.
Thanks to the excellent work of Eric Weinstein, the Equichordal Point Problem
has an entry in the encyclopedia. Here is the link:
http://mathworld.wolfram.com/EquichordalPointProblem.html
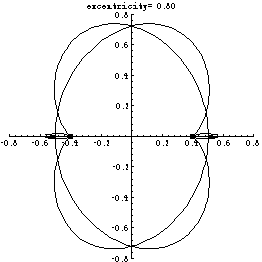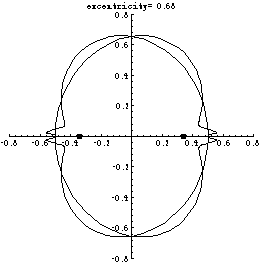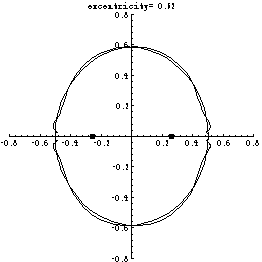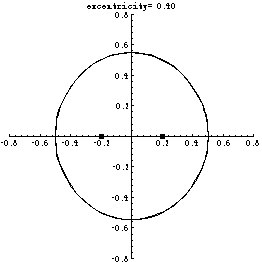
The animation below illustrates a part of the method of the
proof. When one tries to construct a curve with two
equichordal points positioned at a distance $a$ (called
the excentricity, or eccentricity), with the length of the
chords equal to 1, one arrives at two approximating curves,
grown from points (-0.5,0) and (0.5,0) by an iterative
process. In fact, the curves are reflections of each other
in the $y$-axis and are symmetric with respect
to reflections in the $x$-axis.
If for some value of $a$ the curves coincided
then woud have a curve with two equichordal points.
However, the curves oscillate, which prevents them
from coinciding.
The construction of the above animation involves complicated
calculations of series expansions with a CAS, followed by a
numerical iteration process.
The method of Shafke and Volkmer and an earlier work of
Wirsing focus on studying the size of the oscillations of the
potential solutions to the equichordal point problem. It
turns out that they die down with $a$ faster than any
power of $a$. In addition, one can construct
special asymptotic expansions which capture the size of
the oscillations for small $a$.
It proves that the problem reduces to studying properties of
the following functional equation:
$$
\frac{1}{f(\mu z) - f(z) } + \frac{1}{ f(z) - f(z/\mu) } = \frac{1}{a\sqrt{1 + f(z)^2}}
$$

for a complex
function $f(z)$. Here $\mu$ is a
parameter determined from the
equation
$\displaystyle{\mu=\frac{1+a}{1-a}.}$
This function should have a simple pole at $0$ and
it is multi-valued. Its meromorphic continuation can be found
from the above equation. The following picture is obtained if
one plots $|f(z)|$. The color is determined
by $\Re f(z)$.

